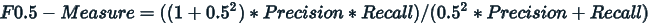Measuring accuracy of the models

Let's get technical. This article looks at how our algorithms weigh relevant elements in text. Here are two important definitions you should understand before diving into the false-positives versus false-negative assessments.

Maximizing precision will minimize false-positive errors. The intuition for precision is that it is not concerned with false negatives and it minimizes false positives. On the other hand, maximizing recall will minimize the false-negative errors. The intuition for recall is that it is not concerned with false positives and it minimizes false negatives.

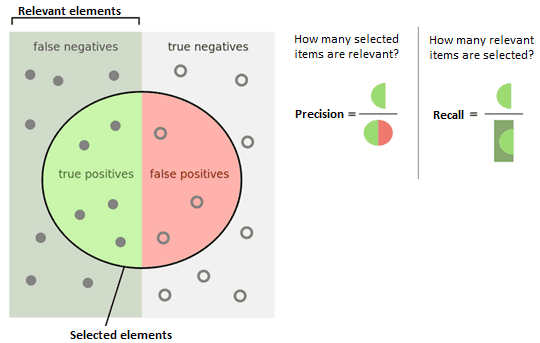
F-measure

F-Measure or F-Score provides a way to combine both precision and recall into a single measure that captures both properties, giving each the same weighting.

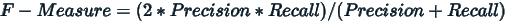
This is the harmonic mean of the two fractions – precision and recall. The F-measure balances the precision and recall. The result is a value between 0.0 for the worst F-measure and 1.0 for a perfect F-measure.

In some cases, we might be interested in an F-measure with more attention put on precision, such as when false positives are more important to minimize, but false negatives are still important. In other cases, we might be interested in an F-measure with more attention put on recall, such as when false negatives are more important to minimize, but false positives are still important.

Fbeta-measure

The Fbeta-measure is a generalization of the F-measure in the sense that it adds a configuration parameter called beta, in other words, an abstraction of the F-measure where the balance of precision and recall in the calculation of the harmonic mean is controlled by a coefficient called beta.

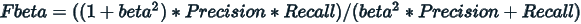
A default beta value is 1.0, which is the same as the F-measure. A smaller beta value than 1.0, such as 0.5, gives more weight to precision and less to recall, whereas a larger beta value than 1.0, such as 2.0, gives less weight to precision and more weight to recall in the calculation of the score.

The F0.5-measure is an example of the Fbeta-measure with a beta value of 0.5.

It has the effect of raising the importance of precision and lowering the importance of recall.

If maximizing precision minimizes false positives, and maximizing recall minimizes false negatives, then the F0.5-measure puts more attention on minimizing false positives than minimizing false negatives.

Our models

All our models run through these formulas and are constantly reviewed to make sure output is optimal. All of our models meet or exceed the following criteria:

• The average precision of all predicted categories is greater than or equal to 0.8.
• Each individual category has a precision that is greater than or equal to 0.6.
• Each model is optimized with a beta equal to 0.5 in FBeta (precision is roughly twice as important as recall).

As new categories are evaluated, we ensure that the above criteria are strictly adhered to ensure that the quality of our predictions remain consistent across all models and all categories within each model.